Loading... # 前言 之前在工作中经常听说模型的预估分和实际分,如果预估分和实际分有较大差异,那么说明模型预测得不是很准确,有调优的空间,但一开始没太明白这是个什么指标。近来有些需求需要延展到这个方面,因此就开始研究这一问题。 # 模型校准 ## 分类模型回顾:以逻辑斯蒂回归模型(LR模型)为例 以经典的二分类的LR模型为例,假设我们的输入向量为$\boldsymbol{x}=(x^{(1)}, x^{(2)}, \cdots, x^{(n)}, 1)^{T}$,权重为$\boldsymbol{w}=(w^{(1)}, w^{(2)}, \cdots, w^{(n)}, b)^{T}$,样本标签为$y$,标签为正例的概率为$p=p(y=1 \mid \boldsymbol{x})$,那么我们预估的LR模型可以表示为 $$ \begin{align*} \log \frac{p}{1-p}=\boldsymbol{w^{T}x} \end{align*} $$ 通过最大似然估计,估计模型参数 $$ \begin{align*} \boldsymbol{w^{*}} = \underset{\boldsymbol{w}}{\operatorname{arg\,max}} \prod_{i=1}^{N} [p(x_{i})]^{y_{i}}[1-p(x_{i})]^{1-y_{i}} \end{align*} $$ 进而可以计算出$p^{*}$。如果我们设定阈值为$\sigma$,那么当$p^{*} \geq \sigma$时我们预测的样本标签为正例,否则为负例 ## 模型评价指标:校准曲线(Calibration Curve) ### 获取模型预测的概率 如果有一定机器学习模型使用经验的同学来说,应该会知道我们解决分类问题的时候,我们除了会获取我们分类模型的标签以外,还可以获取样本属于某类标签的概率。 例如前面的稍加变形有: $$ \begin{align*} p(y=1 \mid \boldsymbol{x})&=\frac{exp(\boldsymbol{w^{T}x})}{1+exp(\boldsymbol{w^{T}x})}\\ p(y=0 \mid \boldsymbol{x})&=\frac{1}{1+exp(\boldsymbol{w^{T}x})}\\ \end{align*} $$ ### 利用预测概率评价模型 实际上不同的模型预测的概率都有一些偏差,比如SVM模型获取模型概率时是通过模型的预测结果,进一步通过某些规则(比如点到直线的距离)去计算概率,这类模型输出的预测概率通常会更多的接近0和1。再比如,在类别不均衡的数据集里,使用1:1采样训练出来的模型,其预测的概率与真实概率的偏差也会比较大。 无论是上述哪种情况,其预测的概率只是保留了概率的相对排序,通过调整合适的阈值,我们可以保证说模型在个体(样本)上有着比较好的预测结果。 但有一些实际问题,我们在实际分析时不仅关注对于个体的预测准确率,还会关注其统计指标利用模型刻画的结果是否准确。比如贷款违约用户识别问题,在做运营分析时,我们不会过度关注某个用户是否被预测准确,而是**更关心预测的用户的违约概率有多高**。再比如,对于网站/页面中的点击预测问题中,**业务方对于单个用户是否点击并不感兴趣,但他们会对网站/页面点击的CTR会很感兴趣**。在这种情况下,我们关注的就不仅仅是预测概率的相对排序了[<sup>[1]</sup>](#ref1)。 基于以上的场景,我们可以引入校准曲线(Calibration Curve)来作为我们额外评价模型的一种标准。校准曲线的使用方法可以通过Niculescu-Mizil等人在2005年发表的论文[<sup>[2]</sup>](#ref2),或者是sklearn中相应的method去详细了解,大致流程如下: - step1: 将对样本按照模型预测概率进行升序排序。 - step2: 将排序后的概率(y_predict_prob)和标签(y_true)分箱,一般来说通常分100个区间(可根据样本数等因素进行调整) - step3: 取每个区间的标签和预测概率的平均值。 - step4: 在y轴上绘制样本标签结果的平均值,在x轴上绘制模型预测概率的平均值,得到校准曲线。 > 注意:Calibration只适用于二分类问题,对于多分类问题,只能是任取两个标签的结果进行评价 例如下图就是一个模型校准曲线的结果。很容易理解,最理想的情况为无论在何种情况下,我们模型预测的概率和实际发生的概率是相同的,在这种情况下,我们可以得到下图中橙色的参考线。而蓝色的校准曲线,即为我们模型预测出的结果。两条线的差异即表示了模型失真的情况 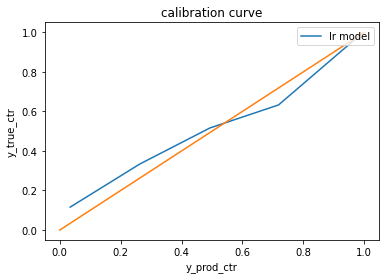 ### 简化版:calibration的计算公式 如果我们的分箱大小为1(bin size=1),衡量模型预测概率与实际概率的偏差可以用下面的公式来表示 $$ \begin{align*} calibration=\frac{avg(predict\_probability)}{avg(true\_click)}-1 \end{align*} $$ **即模型预估概率于实际概率的相对差异**。当$calibration<0$时,说明用户的行为预测被低估,当$calibration>0$时,说明用户的行为预测被高估。**这个指标越接近于0,说明模型预测的结果与实际的结果越接近**。 当我们通过数据分析发现某个特征(feature)可以作为模型的信号时(比如我们发现集数与用户的点击观看率呈现正相关,但当前模型尚未学习),那么可以将该特征加入模型进行训练。之后我们可以用以下指标观测模型的好坏: - 当特征加入模型训练后,如果其calibration比不加该特征时要更接近于0,或者AUC有所提示,说明这个特征可能是有效的 - 通过AB实验,看特征加入后的模型,是否能够给用户的消费体验带来增益 # 参考文献 <div id="ref1"></div> [1] Akshay, G. (2019, September 10). Calibration of Models. https://medium.com/analytics-vidhya/calibration-of-models-afd2d8c1646f <div id="ref2"></div> [2] Niculescu-Mizil, A., & Caruana, R. (2005, August). Predicting good probabilities with supervised learning. In Proceedings of the 22nd international conference on Machine learning (pp. 625-632). 最后修改:2022 年 07 月 03 日 © 允许规范转载 打赏 赞赏作者 赞 0 如果觉得我的文章对你有用,请随意赞赏